Homework

HW1

选择

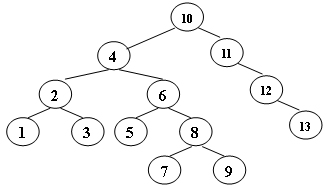
For the result of accessing the keys 3, 9, 1, 5 in order in the splay tree in the following figure, which one of the following statements is FALSE?

A. 5 is the root

B. 1 and 9 are siblings

C. 6 and 10 are siblings

D. 3 is the parent of 4

答案

D 解析：

Consider the following buffer management problem. Initially the buffer size (the number of blocks) is one. Each block can accommodate exactly one item. As soon as a new item arrives, check if there is an available block. If yes, put the item into the block, induced a cost of one. Otherwise, the buffer size is doubled, and then the item is able to put into. Moreover, the old items have to be moved into the new buffer so it costs k+1 to make this insertion, where k is the number of old items. Clearly, if there are N items, the worst-case cost for one insertion can be Ω(N). To show that the average cost is O(1), let us turn to the amortized analysis. To simplify the problem, assume that the buffer is full after all the N items are placed. Which of the following potential functions works?

A.The number of items currently in the buffer

B.The opposite number of items currently in the buffer

C.The number of available blocks currently in the buffer

D.The opposite number of available blocks in the buffer

答案

D 解析：

注意，选择合适的势能函数只要求让每一步的摊销成本为常数，末势能值不一定要大于初势能值

Among the following 6 statements about AVL trees and splay trees, how many of them are correct?

(1) AVL tree is a kind of height balanced tree. In a legal AVL tree, each node's balance factor can only be 0 or 1.

(2) Define a single-node tree's height to be 1. For an AVL tree of height h, there are at most \(2^h−1\) nodes.

(3) Since AVL tree is strictly balanced, if the balance factor of any node changes, this node must be rotated.

(4) In a splay tree, if we only have to find a node without any more operation, it is acceptable that we don't push it to root and hence reduce the operation cost. Otherwise, we must push this node to the root position.

(5) In a splay tree, for any non-root node X, its parent P and grandparent G (guranteed to exist), the correct operation to splay X to G is to rotate X upward twice.

(6) Splaying roughly halves the depth of most nodes on the access path.

答案

（1）AVL树的平衡因子是左子树减去右子树的值，可以是-1，0，1 （2）由于定义单节点的树高度是1，对于一棵高度为h的树，那么最多的节点就是满的，为\(2^h-1\) （3）不一定的，只要平衡因子绝对值不大于1即可 （4）查找一个节点，需要对splay树进行自我调整，如果不调整的话，就没有均摊时间为\(log(n)\)的性质了 （5）zig-zig的情况是先转P和G （6）可以将每次调整的过程看成一种折叠，那么每splay一次就相当于大致把整棵树折叠了一下 错误的有：（1）（3）（4）（5）

Insert { 9, 8, 7, 2, 3, 5, 6, 4 } one by one into an initially empty AVL tree. How many of the following statements is/are FALSE?

• the total number of rotations made is 5 (Note: double rotation counts 2 and single rotation counts 1)
• the expectation (round to 0.01) of access time is 2.75
• there are 2 nodes with a balance factor of -1

A. 0 B. 1 C. 2 D. 3

答案

Insert {3,9,6,1,8,7} into an initially empty splay tree, 7 is the parent of 6

答案

插入完成后的 splay tree 为 7 6,8 3,,,9 1 正确

Amortized bounds are weaker than the corresponding worst-case bounds, because there is no guarantee for any single operation.

Note

单次操作的最差复杂度并不能保证，均摊的界是要比最差的界对每个操作的限制要更r

编程

Root of AVL Tree：给一串输入，找到AVL树的根节点

#include <stdio.h>
#include <stdlib.h>

typedef struct node {
    int val;
    struct node* left;
    struct node* right;
    int height;
} Node;

int max(int a, int b) {
    return a > b ? a : b;
}

int getHeight(Node* node) {
    if (node == NULL) {
        return 0;
    }
    return node->height;
}

Node* Right_rotate(Node* y) {
    Node* x = y->left;
    Node* T2 = x->right;
    x->right = y;
    y->left = T2;
    y->height = max(getHeight(y->left), getHeight(y->right)) + 1;
    x->height = max(getHeight(x->left), getHeight(x->right)) + 1;
    return x;
}

Node* Left_rotate(Node* x) {
    Node* y = x->right;
    Node* T2 = y->left;
    y->left = x;
    x->right = T2;
    x->height = max(getHeight(x->left), getHeight(x->right)) + 1;
    y->height = max(getHeight(y->left), getHeight(y->right)) + 1;
    return y;
}

int getBalanceFactor(Node* node) {
    if (node == NULL) {
        return 0;
    }
    return getHeight(node->left) - getHeight(node->right);
}

Node* insert(Node* root, int val) {
    if (root == NULL) {
        Node* newNode = (Node*)malloc(sizeof(Node));
        newNode->val = val;
        newNode->left = newNode->right = NULL;
        newNode->height = 1;
        return newNode;
    }

    if (val < root->val) {
        root->left = insert(root->left, val);
    } else if (val > root->val) {
        root->right = insert(root->right, val);
    } else {
        return root;
    }

    root->height = 1 + max(getHeight(root->left), getHeight(root->right));
    int balanceFactor = getBalanceFactor(root);

    # 四种旋转情况
    if (balanceFactor > 1 && val < root->left->val) {
        return Right_rotate(root);
    }

    if (balanceFactor < -1 && val > root->right->val) {
        return Left_rotate(root);
    }

    if (balanceFactor > 1 && val > root->left->val) {
        root->left = Left_rotate(root->left);
        return Right_rotate(root);
    }

    if (balanceFactor < -1 && val < root->right->val) {
        root->right = Right_rotate(root->right);
        return Left_rotate(root);
    }

    return root;
}

int main() {
    int n, val;
    scanf("%d", &n);
    Node* root = NULL;
    for (int i = 0; i < n; i++) {
        scanf("%d", &val);
        root = insert(root, val);
    }
    printf("Root value: %d\n", root->val);
    return 0;
}

HW2

选择/判断

2-2

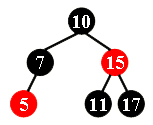
After deleting 15 from the red-black tree given in the figure, which one of the following statements must be FALSE?

A.11 is the parent of 17, and 11 is black

B.17 is the parent of 11, and 11 is red

C.11 is the parent of 17, and 11 is red

D.17 is the parent of 11, and 17 is black

答案

C

2-3

Insert 3, 1, 4, 5, 9, 2, 6, 8, 7, 0 into an initially empty 2-3 tree (with splitting). Which one of the following statements is FALSE?

A.7 and 8 are in the same node

B.the parent of the node containing 5 has 3 children

C.the first key stored in the root is 6

D.there are 5 leaf nodes

答案

A

2-4

After deleting 9 from the 2-3 tree given in the figure, which one of the following statements is FALSE?

A.the root is full

B.the second key stored in the root is 6

C.6 and 8 are in the same node

D.6 and 5 are in the same node

答案

D

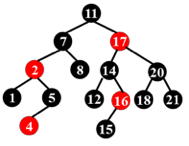
The following binary search tree is a valid red-black tree.

答案

F, 16不满足

A 2-3 tree with 12 leaves may have at most 10 nonleaf nodes

答案

2-3树叶子节点是用来存数据的，12个叶子节点，上一层最多有6个非叶子节点，再上一层最多有3个非叶子节点，再上一层最多一个非叶子节点，共最多10个非叶子节点。

If we insert \(N(N⩾2)\) nodes (with different integer elements) consecutively to build a red-black tree \(T\) from an empty tree, which of the following situations is possible:

A.All nodes in T are black

B.The number of leaf nodes (NIL) in \(T\) is \(2N−1\)

C.\(2N\) rotations occurred during the construction of \(T\)

D.The height of \(T\) is \(⌈3\log_2(N+1)⌉\) (assume the height of the empty tree is 0)

答案

A 显然不可能

B N个节点，算上NIL，只有根节点的度数为2，所以所有点的度数和为 \(3N-1\)，

D 黑色节点最多 N 个黑高最多为 \(⌈\log_2(N+1)⌉\)，所以树高最多 \(⌈2\log_2(N+1)⌉\)

编程

写出一个B+树，可以判断是否有重复元素并最后层序输出全部数据

插入操作：

• 先找到应该插到哪个叶子节点

• 然后在这个叶子节点中找到插入的地方

• 判断这个叶子节点是否满了

没满就直接插入，满了就分裂

分裂操作：

• 分裂叶子：先创建一个叶子，然后把原先叶子的后半部分转移到新的叶子上，然后更新原先叶子与新叶子各自的count值，接着把索引值插入父亲节点上，更新父亲节点的children（如果没有就创建一个新的父亲节点）
• 分裂节点：先创建一个节点，然后分值，分孩子，更新count，接着更新后半部分孩子的父亲。接着将索引拿出给到父亲节点（如果没有需要创建）

分裂的递归思路是找到插入的叶子（记为insertnode），叶子分裂后将索引插入到父亲节点，然后更新insertnode为父亲节点（意思是刚刚被插入数的节点）因为被插入数了所以就要判断这个节点是否需要被分裂，需要分裂就将insertnode继续向上传递，直到分裂结束为止。

由于这个题目要求层序输出，我们在结构体里增加一个next的node指针将每一层节点像链表一样连接起来即可。

# include<stdio.h>
# include<malloc.h>

typedef struct node{
    int data[4];
    int count;
    struct node* children[4];
    struct node* next;
    struct node* parent;
    int isleaf;
}Node;

Node* createnode(int isleaf)
{
    Node* new_node = (Node*)malloc(sizeof(Node));
    new_node->count = 0;
    new_node->isleaf = isleaf;
    for(int i = 0; i < 4; i++)
    {
        new_node->children[i] = (Node*)malloc(sizeof(Node));
        new_node->children[i] = NULL;
    }
    new_node->next = NULL;
    new_node->parent = NULL;
    return new_node;
}

int GetIndex(int* key, int size,int val)
{
    int i;
    for(i = 0; i < size; i++)
    {
        if(key[i]>val)
            break;
    }
    return i;
}

Node* search(Node* root, int val)
{
    if(root==NULL)
        return NULL;
    else if(root->isleaf==1)
        return root;
    else
        return search(root->children[GetIndex(root->data,root->count,val)],val);
}

int searchval(Node* root, int val) {
    if (root == NULL) {
        return 0;
    } else if (root->isleaf == 1) {
        for (int i = 0; i < root->count; i++) {
            if (root->data[i] == val) {
                return 1;
            }
        }
        return 0;
    } else {
        return searchval(root->children[GetIndex(root->data, root->count, val)], val);
    }
}

//插入的时候平移节点中的值用的
void ShiftKey(int* Key, int Begin, int End) 
{
    int i;
    for (i = End; i > Begin; i--) {
        Key[i] = Key[i-1];
    }
}

void ShiftChild(Node** Child,int Begin, int End)
{
    int i;
    for (i = End; i >= Begin; i--) {
        Child[i + 1] = Child[i];
    }
}

//检查插入的节点是否满了
int checkNode(Node* node)
{
    if(node->isleaf==0&&node->count==3)
        return 1;
    if(node->isleaf==1&&node->count==4)
        return 1;
    return 0;
}

//往叶子节点中插入数据
void insertleaf(Node* insertnode,int val)
{
    int pos = GetIndex(insertnode->data,insertnode->count,val);
    ShiftKey(insertnode->data,pos,insertnode->count);
    insertnode->data[pos]=val;
    insertnode->count++;
}

//往非叶子节点中插入数据
void insertnonleaf(Node* insertnode,int val,Node* newchild)
{
    int pos = GetIndex(insertnode->data,insertnode->count,val);
    ShiftKey(insertnode->data,pos,insertnode->count);
    insertnode->data[pos]=val;
    ShiftChild(insertnode->children,pos,insertnode->count);
    insertnode->children[pos+1]=newchild;
    newchild->parent=insertnode;
    insertnode->count++;
}

//分裂叶子节点
void spilitleaf(Node* node)
{
    //创建叶子节点
    Node* newnode=createnode(1);
    //将后半部分移到新节点中
    newnode->data[0]=node->data[2];
    newnode->data[1]=node->data[3];
    //更新count值
    newnode->count=node->count=2;
    //更细next指针，类似于链表操作
    Node* temp=node->next;
    node->next=newnode;
    newnode->next=temp;
    //准备将分裂出来的索引值插入到父亲节点中
    Node* parent=node->parent;
    //如果没有父亲节点
    if(parent==NULL)
    {
        //创建父亲节点
        Node* newparent=createnode(0);
        node->parent=newparent;
        newnode->parent=newparent;
        newparent->children[0]=node;
        newparent->children[1]=newnode;
        newparent->data[0]=newnode->data[0];
        newparent->count=1;
    }
    else
    {
        //直接将索引值插入父亲节点
        insertnonleaf(parent,newnode->data[0],newnode);
    }
}

//分裂非叶子节点
void spilitnonleaf(Node* node)
{
    //创建非叶子节点
    Node* newnode = createnode(0);
    //更新索引
    newnode->data[0]=node->data[2];
    //更新孩子
    newnode->children[0]=node->children[2];
    newnode->children[1]=node->children[3];
    //更新孩子的父亲
    node->children[2]->parent=node->children[3]->parent=newnode;
    newnode->count=node->count=1;
    //更新next
    Node* temp=node->next;
    node->next=newnode;
    newnode->next=temp;
    Node* parent=node->parent;
    //同样的道理创建父亲节点
    if(parent==NULL)
    {
        Node* newparent=createnode(0);
        node->parent=newparent;
        newnode->parent=newparent;
        newparent->children[0]=node;
        newparent->children[1]=newnode;
        newparent->data[0]=node->data[1];
        newparent->count=1;
    }
    else
    {
        insertnonleaf(parent,node->data[1],newnode);
    }
}

//插入操作
Node* insert(Node* root, int val)
{
    //找到val应该插入的叶子节点
    Node* insertnode=search(root,val);
    //如果叶子节点没有（说明刚开始插入）
    if(insertnode==NULL)
    {
        Node* newnode=createnode(1);
        newnode->count=1;
        newnode->data[0]=val;
        return newnode;
    }
    //否则就直接插入节点
    insertleaf(insertnode,val);
    //以insertnode是否满了为循环标准
    while(checkNode(insertnode))
    {
        //如果插入的节点是叶子
        if(insertnode->isleaf==1)
        {
            //分裂叶子节点，并传递insertnode到父亲节点
            spilitleaf(insertnode);
            insertnode=insertnode->parent;
        }
        //如果插入的数非叶子节点
        else
        {
            //分裂非叶子节点，并传递insertnode到父亲节点
            spilitnonleaf(insertnode);
            insertnode=insertnode->parent;
        }
    }
    //如果根节点分裂那么根节点就要发生变化
    if(insertnode->parent==NULL)
        root=insertnode;
    return root;
}

//层序打印整棵树
void printtree(Node* root)
{
    if(root==NULL)
        return;
    Node* ptr=root;
    Node* ptrfirst=root;
    while(ptr!=NULL)
    {
        printf("[");
        for(int i=0;i<ptr->count;i++)
        {
            if(i==ptr->count-1)
                printf("%d",ptr->data[i]);
            else
                printf("%d,",ptr->data[i]);
        }
        printf("]");
        if(ptr->next==NULL)
        {
            printf("\n");
            ptrfirst=ptr=ptrfirst->children[0];
        }
        else
            ptr=ptr->next;
    }
}

int main()
{
    int n;
    scanf("%d",&n);
    Node* root=(Node*)malloc(sizeof(Node));
    root=NULL;
    for(int i=0;i<n;i++)
    {
        int val;
        scanf("%d",&val);
        if(searchval(root,val)==1)
        {
            printf("Key %d is duplicated\n",val);
            continue;
        }
        root=insert(root,val);
    }
    printtree(root);
}

HW3

For the document-partitioned strategy in distributed indexing, each node contains a subset of all documents that have a specific range of index.

答案

T

In a search engine, thresholding for query retrieves the top k documents according to their weights.

答案

F,针对文档的阈值是用来检索权重前多少的文档的，而针对检索的阈值，是将检索的内容按照频率分级后选择部分进行搜索的

Two spam mail detection systems are tested on a dataset with 7981 ordinary mails and 2019 spam mails. System A detects 200 ordinary mails and 1800 spam mails, and system B detects 160 ordinary mails and 1500 spam mails. If our primary concern is to keep the important mails safe, which of the following is correct?

A.Precision is our primary concern and system A is better.

B.Recall is our primary concern and system B is better.

C.Precision is our primary concern and system B is better.

D.Recall is our primary concern and system A is better.

答案

我们要保证重要的文件不被当作垃圾邮件排除掉，我们关注的就应该是precision，A系统的precision为\(1800/2000=0.9\)，B系统的precision为\(1500/1660=0.904\)，所以应该选C

When evaluating the performance of data retrieval, it is important to measure the relevancy of the answer set.

答案

应该是information

HW4

We can perform BuildHeap for leftist heaps by considering each element as a one-node leftist heap, placing all these heaps on a queue, and performing the following step: Until only one heap is on the queue, dequeue two heaps, merge them, and enqueue the result. Which one of the following statements is FALSE?

A.in the k-th run,\(⌈N/2^k⌉\) leftist heaps are formed, each contains \(2^k\) nodes

B.the worst case is when \(N=2^K\) for some integer K

C.the time complexity \(T(N)=O(\frac{N}{2}log2^0+\frac{N}{2^2}log2^1+\dots+\frac{N}{2^K}log2^{K-1})\) for some integer K so that \(N=2^K\)

D.the worst case time complexity of this algorithm is \(Θ(NlogN)\)

Answer

主要想法是，用分治思想来建左式堆。这样建立比一个一个加入要更快 第1轮：大小为1的堆两两合并 第2轮：大小为2的堆两两合并 第3轮：大小为4的堆两两合并 …… 以此类推。 由合并堆的时间复杂度为O（logN），我们很容易写出它的递推式：\(T（N） = 2 T（N/2） + O（logN）\) D 应该为\(O(N)\)

The right path of a skew heap can be arbitrarily long.

答案

T

For a skew heap with N nodes, the worst-case running time of all operations (insert/delete min/merge) is O(N).

答案

T

HW6

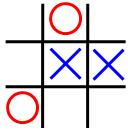
In the Tic-tac-toe game, a "goodness" function of a position is defined as\(f(P)=W_{\text{computer}}−W_{\text{human}}\)where \(W\) is the number of potential wins at position P. In the following figure, O represents the computer and \(X\) the human. What is the goodness of the position of the figure?

答案

B,都是三种

What makes the time complexity analysis of a backtracking algorithm very difficult is that the sizes of solution spaces may vary.

答案

F, 主要是剪枝的问题

HW7

Consider two disjoint sorted arrays A[1…m] and B[1…n], we would like to compute the k-th smallest element in the union of the two arrays, where k≤min{m,n}. Please choose the smallest possible running time among the following options.

A.\(O(\log k)\) B. \(O(\log m)\) C.\(O(\log n)\) D.\(O(\log m+\log n)\)

Answer

A 算法如下： 比较A[k/2]和B[k/2]谁小就可以排除对应的前k/2个得到新的A',B'数组，因为小的那个数组的前k/2个数都不可能为那个第k小的数 再比较A'[k/4]和B'[k/4]，就可以排除k/4 ...依次排除，得到排除次数为log(k) (不够取了就取最大的那个)

Consider the following function, where the time complexity for function calc() is O(1).

void fun(int l, int r) {
    if(r-l+1<=1234) return;
    int m=(l+r)/2;
    int m1=(l+m)/2, m2=(m+1+r)/2;
    fun(l, m);
    fun(m1+1, m2);
    for(int k=1;k<=r-l+1;k++)
        for(int i=1;i<=r-l+1;i++)
            for(int j=l;j<=r;j+=i)
                calc(j, i);
    fun(m+1, r);
    fun(m1+1, m2);
}

Assume the initial input is l=1, r=N, What is the running time of this function? Your answer should be as tight as possible.

A. \(O(Nlog^2N)\) B. \(O(N^{2.5})\) C. \(O(N^2logN)\) D. \(O(N^2log^2N)\)

answer

D \(T(n)=4T(n/2)+n(n+n/2+n/3+...n/(n-1))=4T(n/2)+n^2logn\)

HW8

6-1 Programming Contest

Bob will participate in a programming contest. There are altogether n problems in the contest. Unlike in PAT (Programming Ability Test), in a programming contest one can not obtain partial scores. For problem i, Bob will need time[i] to solve it and obtains the corresponding score[i], or he may choose not to solve it at all. Bob will be happy when he obtains a total score no less than happy_score. You are supposed to find the minimum time needed for Bob to be happy. The function need_time must return the minimum time, or -1 if it is impossible for Bob to obtain a score no less than happy_score.

Format of function:

int need_time(const int time[], const int score[], int happy_score, int n);

Here n (1≤n≤ MAXN) is the number of problems; happy_score (1≤ happy_score ≤ MAXS) is the minimum score for Bob to be happy; time[] is the array to store time[i] (1≤time[i]≤100) which is the time to solve problem i; score[] is the array to store score[i] (1≤score[i]≤100) which is the score Bob gets for solving problem i.

Sample program of judge:

#include <stdio.h>

#define MAXN 10
#define MAXS 1000

int need_time(const int time[], const int score[], int happy_score, int n);

int main() {
  int n, i, happy_score;
  int time[MAXN], score[MAXN];
  scanf("%d %d", &n, &happy_score);
  for (i = 0; i < n; ++i)
      scanf("%d", &time[i]);
  for (i = 0; i < n; ++i)
      scanf("%d", &score[i]);
  printf("%d\n", need_time(time, score, happy_score, n));
  return 0;
}

/* Your function will be put here */

Sample Input:

6 121

84 87 78 16 94 38
87 93 50 22 63 28

Sample Output:

125

Analysis

这是一个0/1背包问题的变种

0/1背包问题背景：给定背包的承重W，一堆物品的重量weights[ ]和价值values[ ]，求背包能装入物品的最大总value

0/1背包问题解法

定义一个二维数组 dp[物品总数][承重+1] 存储当前value，其中 dp[i][j] 表示：从前 i 件物品中找出一些放入背包，在总重不超过承重W的情况下，能达到的最大value。

第 i 件物品重量为 weight[i]，价值为 value[i]，根据第 i 件物品是否添加到背包中，可以分两种情况讨论：

① 第 i 件物品的重量超过背包承重，即 weight[i] > j。此时就算拿出背包中的所有物品也无法放下，所以它不可能被放入背包，因此有：dp[i][j] = dp[i-1][j]

② 第 i 件物品可以添加到背包中（可能拿出一些已有物品）。此时也可以有放入与不放入两种情况，应取value更大的那种。

（2.1）若不放入，有：dp[i][j] = dp[i-1][j]

（2.2）若放入，情况变为从某个状态下加入第i件物品并达到dp[i][j]结果，可知前一状态时的背包承重应为 j-weight[i]。因此有：dp[i][j] = dp[i-1][ j-weight[i]] + value[i]。

综上，递推式为：

  dp[i][j] = max( dp[i-1][j], max( dp[i-1][ j-weight[i] ] + value[i], dp[i-1][j] ) );

即 dp[i][j] = max( dp[i-1][ j-weight[i] ] + value[i], dp[i-1][j] );

dp数组的一维简化：

可以看到不管第 i 件物品有没有加到背包中，新一轮 i 下的dp值都只由 i-1 决定，并且这种决定对于 j 是单方向的（即较大的 j 处的值只和较小或相同的 j 的值有关），因此若 j 从W -> 0 递减，dp的数组可以依次覆盖。

My code

int need_time(const int time[], const int score[], int happy_score, int n)
{
    int sum_1=0;
    int sum_2=0;
    for(int i=0;i<n;i++)
    {
        sum_1+=score[i];
        sum_2+=time[i];
    }
    if (sum_1<happy_score)
        return -1;
    sum_1=sum_1-happy_score;
    int* dp=(int*)malloc(sizeof(int)*(sum_1+1));
    //这里的dp[j]代表的是分数不超过j的最大时间数
    for(int i=0;i<=sum_1;i++)
        dp[i]=0;
    for(int i=0;i<n;i++)
    {
        //每经过一次循环，新增一样物品score[i]可以放到包里
        for(int j=sum_1;j>=0;j--)
        {
            //对于j>=score[i]的dp我们可以从中拿出题并放入score[i]，否则拿不出来
            if (j>=score[i])
            {
                //看看放入score[i]能不能增加time
                dp[j]=max(dp[j],dp[j-score[i]]+time[i]);
            }
        }
    }
    return sum_2-dp[sum_1];
}

HW9

Consider the problem of making change for n cents using the fewest number of coins. Assume that each coin's value is an integer. The coins of the lowest denomination（面额） is the cent.

(I) Suppose that the available coins are quarters (25 cents), dimes (10 cents), nickels (5 cents), and pennies (1 cent). The greedy algorithm always yields an optimal solution.

(II) Suppose that the available coins are in the denominations that are powers of c, that is, the denominations are \(c^0, c^1, ..., c^k\) for some integers c>1 and k>=1. The greedy algorithm always yields an optimal solution.

(III) Given any set of \(k\) different coin denominations which includes a penny (1 cent) so that there is a solution for every value of n, greedy algorithm always yields an optimal solution.

Which of the following is correct?

A. Statement (I) is false.

B. Statement (II) is false.

C. Statement (III) is false.

D. All of the three statements are correct.

Note

第三个是错的，比若说我需要 10 cents，coins的面额分别是 6，5，1, 如果按照贪心的做法，应该是 \(6+1\times4\)，事实上最好的方法应该是 \(5\times 2\)

HW10

All the languages can be decided by a non-deterministic machine.

Note

F，并不是所有语言都可以被非确定性图灵机所验证

All NP problems can be solved in polynomial time in a non-deterministic machine.

Note

T，而所有NP问题都可以被非确定性图灵机所验证，因为非确定性图灵机的每一步都是正确的

If a problem can be solved by dynamic programming, it must be solved in polynomial time.

Note

能用动态规划做的问题不一定可以被多项式解决，因为动态规划得到的复杂度可能和问题中的某个参数有关，这个参数确可以无限大

Suppose Q is a problem in NP, but not necessarily NP-complete. Which of the following is FALSE?

A. A polynomial-time algorithm for SAT would sufficiently imply a polynomial-time algorithm for Q.

B. A polynomial-time algorithm for Q would sufficiently imply a polynomial-time algorithm for SAT.

C. If \(Q \notin P\), then \(P\neq NP\).

D. If Q is NP-hard, then Q is NP-complete.

答案

A. 由于 SAT 问题为 NPC 问题，那么 Q 问题可以被多项式规约为 SAT 问题，而如果 SAT 问题存在多项式算法，那么 Q 问题也有相应的多项式算法

B. A 选项反过来就不能这么说了

C选项是显然的，D是因为 Q 是 NP 问题

综上，本题应该选择 B

NP-complete problems are the hardest problems in NP-hard problems in terms of computational complexity.

答案

F, 两者都是可被所有NP问题规约而来，所以所有 NP-hard 问题都可以被 NPC 问题多项式转化，但是这也并不能说明 NP-hard 比 NPC 问题难。

HW11

Suppose ALG is an \(α\)-approximation algorithm for an optimization problem \(Π\) whose approximation ratio is tight. Then for every \(\varepsilon>0\) there is no \((α−\varepsilon)\)-approximation algorithm for \(Π\) unless P = NP.

答案

这里近似比 \(\alpha\) 针对的是 ALG 这个算法的最佳近似比，而这并不代表该问题不存在更好的近似比的解法，比如说对与装箱问题来说，next-fit的解法的最佳近似比就是2，而first-fit的解法的最佳近似比就可以小于2.

As we know there is a 2-approximation algorithm for the Vertex Cover problem. Then we must be able to obtain a 2-approximation algorithm for the Clique problem, since the Clique problem can be polynomially reduced to the Vertex Cover problem.

答案

注意问题可以相互转化，但是近似比不能相互转化！

To approximate a maximum spanning tree T of an undirected graph \(G=(V,E)\) with distinct edge weights \(w(u,v)\) on each edge \((u,v)∈E\), let's denote the set of maximum-weight edges incident on each vertex by S. Also let \(w(E′)=\sum_{(u,v)∈E′}w(u,v)\) for any edge set \(E′\). Which of the following statements is TRUE?

A. \(S=T\) for any graph \(G\)

B. \(S\ne T\) for any graph \(G\)

C. \(w(T)≥w(S)/2\) for any graph \(G\)

D. None of the above

答案

S 包括的是每个点出射的最大权重的边，这个与T可能相同也可能不相同

S 最多 n-1 条边，因为每个点会选择一条边，同时对于最大的那条边会有两个点选择它这条边，所以 S 最多有 n-1 条边。

而对于最大生成树 T 来说，我们采用 Kruskal 算法，每次选择不成环的最大的那条边。如果我们选择的这条边引入了一个新的点，那么新加进来的这条边一定属于S；如果我们新引入的这条边未引入一个新的点，那么说明S已经被全部引入到T中（为什么？因为如果存在S中的一条边不在T中，那么对应的那个点是由另一条边而引入T中的，这是不可能的）。这样我们就说明了 \(w(T)≥w(S)\)

于是该问题应该选C

Assume that you are a real world Chinese postman, which have learned an awesome course "Advanced Data Structures and Algorithm Analysis" (ADS). Given a 2-dimensional map indicating N positions \(p_i(x_i,y_i)\) of your post office and all the addresses you must visit, you'd like to find a shortest path starting and finishing both at your post office, and visit all the addresses at least once in the circuit. Fortunately, you have a magic item "Bamboo copter & Hopter" from "Doraemon", which makes sure that you can fly between two positions using the directed distance (or displacement).

However, reviewing the knowledge in the ADS course, it is an NPC problem! Wasting too much time in finding the shortest path is unwise, so you decide to design a 2−approximation algorithm as follows, to achieve an acceptable solution.

Compute a minimum spanning tree T connecting all the addresses.
Regard the post office as the root of T.
Start at the post office.
Visit the addresses in order of a _____ of T.
Finish at the post office.

There are several methods of traversal which can be filled in the blank of the above algorithm. Assume that \(P\ne NP\), how many methods of traversal listed below can fulfill the requirement?

• Level-Order Traversal
• Pre-Order Traversal
• Post-Order Traversal

A. 0 B. 1 C. 2 D. 3

Answer

C,level-order traversal不行

注意到最短路径一定比MST要大，而其他两个的走法最多一条边走两次，不会超过2倍的MST，但是level-order就说不准了，可能一条边要走好多次

Revisit the activity selection problem. Given a set of activities \(S={a_1,a_2,⋯,a_n}\) that wish to use a resource, each \(a_i\) takes place during a time interval. The goal is to arrange as many compatible activities as possible. Recall that several greedy approaches are introduced in the class, among which the one selecting an activity with the shortest length, denoted by \(SF\), is not always optimal. However, we claim that \(SF\) accepts at least \(∣OPT∣/2\) activities, given that the optimal value is \(∣OPT∣\), where \(OPT\) is an optimal solution. Check if the following is a correct proof.

We use a technique, called the charging scheme, similarly as the amortized analysis. Suppose each accepted activity of \(OPT\) holds one dollar, which will be given to the activities accepted by \(SF\) in the following way. For any activity \(a_i\) of \(OPT\), if \(a_i\) is also accepted by \(SF\), give the dollar to itself. Otherwise, there must be some activity \(a_j\), accepted by \(SF\), is not compatible with \(a_i\). Then \(a_j\) receives one dollar from \(a_i\). Along this line, each activity of \(OPT\) sends out one dollar to an activity in \(SF\), while each activity of \(SF\) receives at most two dollars. It implies that \(SF\) accepts as least \(∣OPT∣/2\) activities.

Note

T,这个类似于摊还分析的分析方式为设每一个OPT中的活动有一美元，如果OPT中的活动在SF中出现了，那么给1美元。如果一个活动在OPT中出现，但是在SF中没有出现，那么给SF中与该活动有重复的活动一美元。

本题目的关键在于在没有出现在SF中的OPT活动，该活动最多与SF中的两个有重复，否则根据OPT的选取规则，我应该会选择中间更短的那个活动

In the bin packing problem, we are asked to pack a list of items L to the minimum number of bins of capacity 1. For the instance \(L\), let \(FF(L)\) denote the number of bins used by the algorithm First Fit. The instance \(L'\) is derived from \(L\) by deleting one item from \(L\). Then \(FF(L')\) is at most of \(FF(L)\).

答案

F，反例如下：Bin size = 1

L = {0.55,0.7,0.55,0.1,0.45,0.15,0.3,0.2}

L' = L- {0.1} = {0.55,0.7,0.55,0.45,0.15,0.3,0.2}

L 的情况只用了三个，而L'的情况却用了4个

For an approximation algorithm for a minimization problem, given that the algorithm does not guarantee to find the optimal solution, the best approximation ratio possible to achieve is a constant \(α>1\).

答案

近似比可以无限差，比如说没有限制的TSP问题

Consider the bin packing problem which uses a minimum number of bins to accommodate a given list of items. Recall that Next Fit (NF) and First Fit (FF) are two simple approaches, whose (asymptotic) approximation ratios are 2 and 1.7, respectively. Now we focus on a special class \(I2\) of instances in which only two distinct item sizes appear. Check which of the following statements is true by applying NF and FF on \(I2\).

A. NF and FF both have improved approximation ratios.

B. NF has an improved approximation ratio, while FF does not.

C. FF has an improved approximation ratio, while NF does not.

D. Neither of NF or FF has an improved approximation ratio.

答案

貌似选C，等会再看

Assume P≠NP, please identify the false statement.

A. There cannot exist a \(ρ-approximation\) algorithm for bin packing problem for any \(ρ<3/2\).

B. In the minimum-degree spanning problem, we are given a graph G=(V, E) and wish to find a spanning tree T of G so as to minimize the maximum degree of nodes in T. Then it is NP-complete to decide whether or not a given graph has minimum-degree spanning tree of maximum degree two.

C. In the minimum-degree spanning problem, we are given a graph \(G=(V, E)\) and wish to find a spanning tree T of G so as to minimize the maximum degree of nodes in T. Then there exists an algorithm with approximation ratio less than 3/2.

D. In the knapsack problem, for any given real number \(ϵ>0\), there exists an algorithm with approximation ratio less than \(1+ϵ\).

答案

选C

A. 装箱问题不可能存在近似比小于3/2的多项式算法，这是因为分箱问题（将一堆物品分成等重的两部分）是一个NPC问题

B. 判断是否存在最大度数为2的最小生成树等价于哈密顿路径问题，而这个是 NPC 问题

C. 不可能存在近似比小于3/2的多项式算法，如果存在，那么我就可以用其来解决哈密顿路径问题

D. 背包问题可用一个 \(\varepsilon\) 来控制精度

In the bin packing problem, suppose that the maximum size of the items is bounded from above by \(α<1\). Now let's apply the Next Fit algorithm to pack a set of items L into bins with capacity 1. Let \(NF(L)\) and \(OPT(L)\) denote the numbers of bins used by algorithms Next Fit and the optimal solution. Then for all \(L\), we have \(NF(L)<ρ⋅OPT(L)+1\) for some \(ρ\). Which one of the following statements is FALSE?

A. \(ρ=\frac{1}{1-\alpha}\), if \(0≤α≤1/2\).

B. \(ρ=2\), if \(α>1/2\).

C. If \(L\) = (0.5, 0.3, 0.4, 0.8, 0.2, 0.3), then \(NF(L)=4\).

D. \(ρ=2α\) if \(0≤α≤1\)

答案

选择 D

A. 最大的物品不会超过 \(\alpha\), 那么每个箱子至少有 \(1-\alpha\) 的货物，那么当\(0≤α≤1/2\) 时，物品总重至少 \((1-\alpha)\times NF(L)\)，那么相应的最佳值肯定至少为该值，相应的近似比就是 \(\frac{1}{1-\alpha}\)

B. 而对于 \(α>1/2\) 的情况就按照上课讲的内容来求近似解

HW12

For the graph given in the following figure, if we start from deleting the black vertex, then local search can always find the minimum vertex cover.

Note

我们从黑色的点开始删除，那么接下来可以删除的就是下方的两个点，这都能得到最优的情况

Spanning Tree Problem: Given an undirected graph \(G=(V,E)\), where \(|V|=n\) and \(|E|=m\). Let \(F\) be the set of all spanning trees of \(G\). Define \(d(u)\) to be the degree of a vertex \(u∈V\). Define w(e) to be the weight of an edge \(e∈E\).

We have the following three variants of spanning tree problems:

• (1) Max Leaf Spanning Tree: find a spanning tree T∈F with a maximum number of leaves.
• (2) Minimum Spanning Tree: find a spanning tree T∈F with a minimum total weight of all the edges in T.
• (3) Minimum Degree Spanning Tree: find a spanning tree T∈F such that its maximum degree of all the vertices is the smallest.

For a pair of edges \((e,e')\) where \(e∈T\) and \(e'∈(G−T)\) such that \(e\) belongs to the unique cycle of \(T∪e'\), we define edge-swap(\(e,e'\)) to be \((T−e)∪e'\).

Here is a local search algorithm:

T = any spanning tree in F;
while (there is an edge-swap(e, e') which reduces Cost(T)) {
    T = T - e + e';
}
return T;

Here Cost(T) is the number of leaves in T in Max Leaf Spanning Tree; or is the total weight of T in Minimum Spanning Tree; or else is the minimum degree of T in Minimum Degree Spanning Tree.

Which of the following statements is TRUE?

A. The local search always return an optimal solution for Max Leaf Spanning Tree

B. The local search always return an optimal solution for Minimum Spanning Tree

C. The local search always return an optimal solution for Minimum Degree Spanning Tree

D. For neither of the problems that this local search always return an optimal solution

Note

应该只有 B 是可以证明的，其他两个应该都存在那些非极小值点，但不是最小值的点

Consider the Minimum Degree Spanning Tree problem: Given a connected undirected graph \(G(V,E)\), find a spanning tree \(T\) whose maximum degree over its vertices is minimized over all spanning trees of \(G\). The problem can be shown to be NP-hard by reduction from the Hamiltonian Path Problem. On the other hand, we can use local search to design approximating algorithms. Denote \(d(u)\) as the degree of vertex \(u\) on a tree \(T\). Consider the following algorithm:

1. Find an arbitrary spanning tree \(T\) of \(G\).
2. If there's some edge \(e∈E(G)-E(T)\) with endpoints \(u,v\), and there's some other vertex \(w\) on the path between \(u,v\) on \(T\) such that \(\max\{d(u),d(v)\}+1<d(w)\), then we replace an edge \(e'\) incident to \(w\) on \(T\) with \(e\), i.e. \(T:=T∪{e}-\{e’\}\).
3. Repeat Step (2) until there's no edge to replace.

It can be shown that this algorithm will terminate at a solution with maximum vertex degree \(OPT+O(\log∣V∣)\). To show the algorithm will terminate in finite steps, a useful technique is to define a nonnegative potential function \(ϕ(T)\) and to show \(ϕ(T)\) is strictly decreasing after each step. Which of the following potential functions below satisfies the above requirements?

A. \(\phi(T) = \sum_{v \in V} d(v)\).

B. \(\phi(T) = \sum_{(u,v) \in E(T)} \max\{d(u), d(v)\}\).

C. \(\phi(T) = \sum_{u \in V} \sum_{v \in V, v \neq u} \sum_{w \in V, w \neq u, v} \max\{d(u), d(v), d(w)\}\).

D. \(\phi(T) = \sum_{v \in V} 3^{d(v)}\).

答案

应该选D

这个题目的意思是从T的补图中选择一条边e，两个顶点分别是u，v；然后w是u,v在T中的经过路径的一个中间点，我们选择w发出的一条边e'与e进行替换 只有D是严格递减的

要注意我们这番操作不仅与u，v，w有关，还与e'连接的另一个点有关，其他几个选项都会被这个点所影响

Consider the metric Facility Location problem. A company wants to distribute its product to various cities. There is a set \(I\) of potential locations where a storage facility can be opened and a fixed “facility cost” \(f_i\) associated with opening a storage facility at location \(i∈I\). (Sometimes we will say “facility \(i\)” to mean “facility at location \(i\)”). There also is a set \(J\) of cities to which the product needs to be sent, and a “routing cost” \(c(i,j)\) associated with transporting the goods from a facility at location \(i\) to city \(j\). The goal is to pick a subset \(S\) of \(I\) so that the total cost of opening the facilities and transporting the goods is minimized. In short, we want to minimize \(C(S)=C_f(S)+C_r(S)\), where \(C_f(S)=∑{i∈S}fi\) and \(Cr(S)=∑_{j∈J}\min_{i∈S}c(i,j)\). Consider the following local serach algorithm:

1. Picking any subset \(S\) of the set \(I\) of facilities. This give us a feasible solution right away.
2. We then search for the local neighborhood of the current feasible solution to see if there is a solution with a smaller objective value; if we find one we update our feasible solution to that one.
3. We repeat step 2 until we do not find a local neighbor that yields a reduction in the objective value.

There are two types of “local steps” that we take in searching for a neighbor: i) remove/add a facility from/to the current feasible solution, or ii) swap a facility in our current solution with one that is not.

Which of the following statement is true?

A. This algorithm is 2-approximation.

B. Let \(S\) be a local optimum that the above algorithm terminates with, and \(S^∗\) be a global optimum. Then \(C_r(S)≥C(S^∗)\).

C. Let \(S\) be a local optimum that the above algorithm terminates with, and \(S^∗\) be a global optimum. Then \(C_r(S)≤C(S^∗)\).

D. None of the other options are correct.

答案

我感觉应该选C

HW13

Let \(a=(a_1,a_2,…,a_i,…,a_j,…,a_n)\) denote the list of elements we want to sort. In the quicksort algorithm, if the pivot is selected uniformly at random. Then any two elements get compared at most once and the probability of \(a_i\) and \(a_j\) being compared is \(2/(j−i+1)\) for \(j>i\), given that \(a_i\) or \(a_j\) is selected as the pivot.

答案

F,举反例如下：{3, 4, 1, 2,}。如果第一次选 pivot 选中 3 或者 2，那么 1 和 4 会被分开，不会被比较。

如果第一次就选中 1 或 4，它们才会被比较。因此它们被比较的概率是 ½。按照 \(2/(j−i+1)\) 计算，应该是 1。

事实上，如果是已经被排序好的，这就是对的，也就是说这里的i,j指的是第i大以及第j大时，结论是成立的

The Online Hiring Algorithm ( hire only once ) is described as the following:

int OnlineHiring ( EventType C[ ], int N, int k )
{
    int Best = N;
    int BestQ = -INFINITY ;
    for ( i=1; i<=k; i++ ) {
        Qi = interview( i );
        if ( Qi > BestQ )   BestQ = Qi;
    }
    for ( i=k+1; i<=N; i++ ) {
        Qi = interview( i );
        if ( Qi > BestQ ) {
            Best = i;
            break;
        }
    }
    return Best;
}

Assume that the quality input \(C[~]\) is uniformly random. When \(N\) = 271 and \(k\) = 90, the probability of hiring the \(N\) th candidate is__.

A.1/e

B.1/N

C.1/3

D.1/k

答案

我们要把它分为两种情况，一种是刚好最后一个就是最大的，另一种是最大的在前k个，最后一个是迫不得已选的。分别计算概率得到 \(1/3\)

Given a linked list containg \(N\) nodes. Our task is to remove all the nodes. At each step, we randomly choose one node in the current list, then delete the selected node together with all the nodes after it. Here we assume that each time we choose one node uniformly among all the remaining nodes. What is the expected number of steps to remove all the nodes?

A.\(Θ(\log N)\)

B.\(N/e\)

C.\(N/2\)

D.\(\sqrt N\)

答案

这个题的意思是要删掉所有节点，删除的方式是随机选取一个点，将它和它之后的节点都删掉。得到相应的关系式

\[ a_n=\frac{1}{N}\sum_{i=1}^{N-1}a_i+O(1) \]

A randomized Quick-sort algorithm has an \(O(N\log N)\) expected running time, only if all the input permutations are equally likely.

答案

F，随机快排应该与输入没什么关系，只要每次的选择是随机的就行

HW14

In order to solve the maximum finding problem by a parallel algorithm with \(T(n)=O(1)\) , we need work load \(W(n)=Ω(n^2)\) in return.

答案

F，我们使用随机选择那个方法就可以做到 O(n) 的workload

HW15

If only one tape drive is available to perform the external sorting, then the tape access time for any algorithm will be \(Ω(N^2)\).

答案

T, 考虑寻道时间从 \(O(1)\) 上升到了 \(O(n)\)，而对于每个数据都需要访问，所以复杂度至少为 \(\Omega(N^2)\)

Given 100,000,000 records of 256 bytes each, and the size of the internal memory is 128 MB. If simple 2-way merges are used, how many passes do we have to do?

A. 10

B. 9

C. 8

D. 7

答案

\[ 1+\lceil \log_2(\frac{10000000}{128\times2^10/256})\rceil=9 \]

Suppose we have the internal memory that can handle 12 numbers at a time, and the following two runs on the tapes:

Run 1: 1, 3, 5, 7, 8, 9, 10, 12

Run 2: 2, 4, 6, 15, 20, 25, 30, 32

Use 2-way merge with 4 input buffers and 2 output buffers for parallel operations. Which of the following three operations are NOT done in parallel?

A. 1 and 2 are written onto the third tape; 3 and 4 are merged into an output buffer; 6 and 15 are read into an input buffer

B. 3 and 4 are written onto the third tape; 5 and 6 are merged into an output buffer; 8 and 9 are read into an input buffer

C. 5 and 6 are written onto the third tape; 7 and 8 are merged into an output buffer; 20 and 25 are read into an input buffer

D. 7 and 8 are written onto the third tape; 9 and 15 are merged into an output buffer; 10 and 12 are read into an input buffer

Note

评论区

对你有帮助的话请给我个赞和 star =>
欢迎跟我探讨！！！