2024 2025 秋期中考试
判断¶
1-1
In a Turnpike Reconstruction Problem, given distance set D = { 1,2,3,4,5,6 } , \((x_1,…,x_4)\)=(0,1,4,6) is the only solution provided that \(x_1\)=0.
Answer
F
1-2
After inserting { 1, 2, 3, 4, 5, 6, 7 } into an initially empty red-black tree, then the number of black nodes in the red-black tree is 4.
Answer
T
1-3
The null path length, Npl(X), of any node X is the length of the shortest path from X to a node without two children.
Answer
T
1-4
For a B+ tree with order M and N keys, the time complexity of find operations is \(O(log_MN)\)
Answer
F
1-5
Insert {3,9,6,1,8,7} into an initially empty splay tree, 7 is the parent of 6.
Answer
T
1-6
Inserting a node into a binomial heap with 9 nodes costs less time than inserting a number into a binomial heap with 15 nodes.
Answer
T
1-7
In dynamic programming algorithms, some results of subproblems have to be stored even they do not compose the optimal solution of a larger problem.
Answer
T
1-8
By the master theorem, the solution to the recurrence \(T(n)=3T(n/4)+nlogn\) is \(O(nlogn)\)
Answer
T
1-9
In explosive detection at a station, Precision is usually more important than Recall.
Answer
F
1-10
There exists an AVL tree of depth (the depth of the root is 0) 6 and 31 nodes.
Answer
F
选择¶
2-1
Consider the following merge algorithm for skew heaps. A merge is performed using a simple routine: merging two skew heaps A and B, if the top of A is less than or equal to the top of B, A becomes the skew heap, its children are swapped and B is merged with the left sub-heap of the root of A. If the left sub-heap is empty, B is assigned to the left sub-heap of A.
A node p is heavy if the number of descendants of p’s right subtree is at least half of the number of descendants of p, and light otherwise. The potential function is defined to be the number of heavy nodes. Let heap A and heap B be a n-node tree.
Which of the following is FALSE?
A. All heavy nodes in the right path of A and B will become the light nodes after merging.
B. The amortized running time of merge is \(O(logn)\).
C. The only nodes whose heavy/light status can change are nodes that are initially on the right path.
D. There are at most \(O(logn)\) light nodes in the right path of a n-node tree.
Answer
A
2-2
Insert { 5, 6, 1, 7, 0, 4, 2, 3, 9 } into an initially empty 2-3 B tree (with splitting). Which one of the following statements is FALSE?
A. there are 4 leaf nodes
B. the key stored in the root is 4
C. 6 and 7 are in the same node
D. the leaf node containing 6 has 3 children
Answer
D
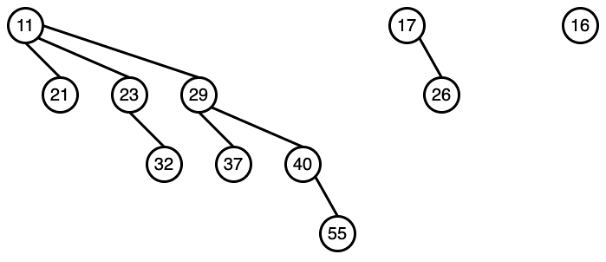
2-3
Delete the minimum number from the binomial queue given in the following figure. Which one of the following statements must be FALSE? (Note that you can merge any two of carry, T1 and T2 when all of them are not none)
A. 29 must have the sibling 26
B. 21 must be the child of 16
C. 16, 17 may be the root of some binomial trees
D. After deletion there are no B2 binomial tree in the binomial queue
Answer
A
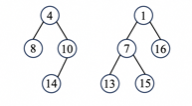
2-4
Merge the two leftist heaps in the figure. How many of the following statements is/are FALSE ?
- 8 and 10 are siblings
- 7 and 4 are siblings
- 4 and 10 have the different NPL
- along the left path from the root, we have 1, 4, 10, 16
A. 1
B. 3
C. 0
D. 2
Answer
D
2-5
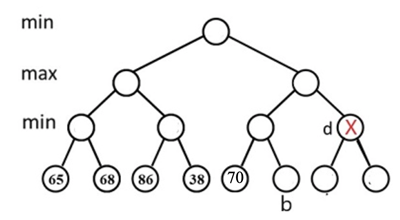
Given the following game tree, node d will be pruned with α−β pruning algorithm if and only if _____.
A. 65 ≤ b ≤ 70
B. b ≥65
C. 70 ≤ b ≤ 86
D. b ≥ 38
Answer
B
2-6
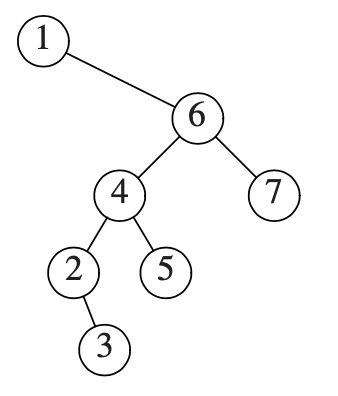
For the result of accessing the keys 4 and 7 in order in the splay tree given in the figure, which one of the following statements is FALSE?
A. 5 and 1 are siblings
B. 2 and 4 are siblings
C. 7 is the root
D. 2 is the parent of 3
Answer
B
2-7
In the context of Red-Black Tree, how many of the following statements are True?
- In the worst case the DELETE operation in a Red-Black tree of nodes requires \(Ω(logn)\) rotations.
- In a Red-Black tree with 3 internal nodes, there must be a red internal node.
- When inserting a node into a red-black tree, we shall first insert the node as into an ordinary binary search tree, and then color the node black.
- In a Red-Black tree, the path from the root to the nearest leaf is no more than half as long as the path from the root to the farthest leaf.
A. 1
B. 3
C. 0
D. 2
Answer
C
2-8
In this problem, we would like to find the amortized cost of insertion in a dynamic table T. Initially the size of the table T is 1. The cost of insertion is 1 if the table is not full. When an item is inserted into a full table, the table T is expanded as a new table of size 5 times larger. Then, we copy all the elements of the old table into this new table, and insert the item in the new table.
Let num(T) be the number of elements in the table T, and size(T) be the total number of slots of the table. Let \(D_i\) denote the table after applying the \(i\) th operation on \(D_{i−1}\).
Which of the following potential function \(Φ(D_i)\) can help us achieve \(O(1)\) amortized cost per insertion?
A. \(Φ(D_i)=num(T)-\frac{size(T)}{5}\)
B. \(Φ(D_i)=num(T)+\frac{size(T)}{5}\)
C.\(Φ(D_i)=\frac{5}{4}(num(T)-\frac{size(T)}{5})\)
D.\(Φ(D_i)=\frac{5}{4}(num(T)-\frac{size(T)}{5})\)
Answer
C
2-9
Which of the asymptotic upper bound for the following recursive T(n) is correct?
A. \(T(n)=2T(n)+logn\). Then \(T(n)=O(lognlogn)\)
B. \(T(n)=3T(n/2)+n\). Then \(T(n)=O(nlogn)\)
C. \(T(n)=2T(n/2)+nlog_2n\). Then \(T(n)=O(nlog_2n)\).
D. \(T(n)=T(n^{1/3})+T(n^{2/3})+logn\). Then \(T(n)=O(logn loglogn)\).
Answer
D
编程¶
3-1
Given an integer array nums, you need to find the length of the longest strictly increasing subsequence in nums.
A subsequence is a sequence derived from the array by deleting some or no elements without changing the order of the remaining elements. For example, [3, 6, 2, 7] is a subsequence of the array [0, 3, 1, 6, 2, 2, 7].
We use dynamic programming to solve the problem. Please fill up the blanks in the following program:
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 10000
int max(int a, int b) {
return (a > b) ? a : b;
}
int lengthOfLIS(int* nums, int numsSize) {
if (numsSize <= 1) return numsSize;
int dp[MAX_SIZE];
for(int i = 0; i < numsSize; i++) {
dp[i] = 1;
}
int result = 1;
for(int i = 1; i < numsSize; i++) {
for(【填空1】) {
if(nums[i] > nums[j]) {
【填空2】;
}
if(dp[i] > result) {
result = dp[i];
}
}
}
return result;
}
Answer
填空1:int j=0;j<i;j++
填空2:dp[i]=dp[j]+1
3-2
You are tasked with solving the classic Eight Queens Problem, where the goal is to place eight queens on an 8×8 chessboard such that no two queens threaten each other. This means that no two queens share the same row, column, or diagonal. We will use the backtracking method to solve this problem. Please fill in the blanks in the following C functions to complete the algorithm.
#include <stdio.h>
#include <stdbool.h>
#define N 8
int solutions = 0;
bool isSafe(int board[N][N], int row, int col) {
int i, j;
for(i = 0; i < row; i++) {
if(board[i][col]) return false;
}
for(i = row-1, j = col-1; i >=0 && j >=0; i--, j--) {
if(board[i][j]) return false;
}
for(i = row-1, j = col+1;【填空1】) {
if(board[i][j]) return false;
}
return true;
}
void solveNQueens(int board[N][N], int row) {
if(row == N) {
solutions++;
}
for(int col = 0; col < N; col++) {
if(isSafe(board, row, col)) {
board[row][col] = 1;
solveNQueens(【填空2】);
【填空3】;
}
}
}
int main() {
int board[N][N];
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
board[i][j] = 0;
}
}
solveNQueens(board, 0);
printf("%d", solutions);
return 0;
}
Answer
填空1:i>=0 &&j<=N-1;i--,j++
填空2:board,row+1
填空3:board[row][col]=0